Chi-Square Distribution

Chi-Squared Distribution

pdf

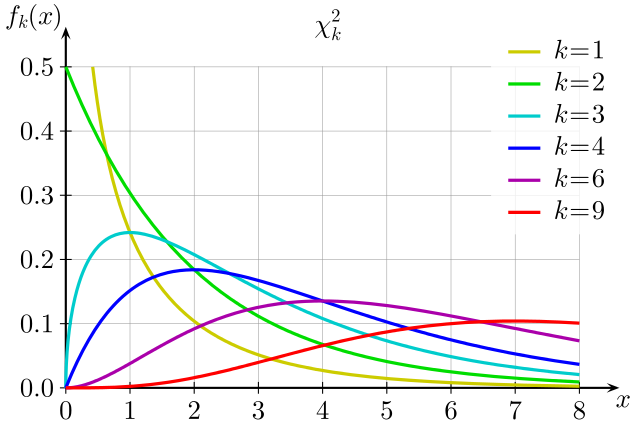
If $Z_1,\dots ,Z_n$ are IID standard normal random variables, then

$$X=\sum _{i=1}^n{Z}_i^2$$

is said to have a chi-square distribution with $n$ degrees of freedom.

By the uniqueness of MGF, chi-square distribution with $n$ degrees of freedom is Gamma Distribution with parameter $(n/2,1/2)$.

• Notation
  • ${\chi }_n^2$
• Parameters
  • $n$
• MGF
  • $(1-2t{)}^{-n/2}$
• PDF

  • $f(x)=\frac{e^{-x/2}(x/2{)}^{n/2-1}}{2\Gamma (n/2)},x\ge 0$

  • 💡 This PDF gives $f(x)=0$ when $n>2$, $f(x)=1/2$ when $n=2$, and $f(x)=\infty$ when $n<2$.

• Mean
  • $n$
• Variance
  • $2n$

Examples

Sample Variance

Let $S_n^2=\frac{1}{n-1}{\sum }_{i=1}^n(X_i-\overline{X}{)}^2$ be the unbiased variance estimator, where $X_i\sim \mathcal{N}(\mu ,{\sigma }^2)$. Then, the following random variable is chi-square distributed:

$$\frac{(n-1)S_n^2}{{\sigma }^2}=\frac{1}{{\sigma }^2}\sum _{i=1}^n(X_i-\overline{X}{)}^2\sim {\chi }_{n-1}^2.$$

The result follows from Cochran’s theorem, which also tells us that $S_n^2$ and $\overline{X}$ are independent.