Fisher Information

Fisher information is a concept in statistics that measures the amount of information that a random variable carries about an unknown parameter. Fisher information of a parameter is the variance of the Score Function:

$$I(\theta )=\mathrm{Var}\left(\frac{\partial }{\partial \theta }\log f(X;\theta )\right).$$

If the Statistical Model is well-specified, and the regularity allows the exchange of integral and derivation, we have that the expectation of the score function is always zero:

$$\mathbb{E}\left[\frac{\partial }{\partial \theta }\log f(X;\theta )\right]=\int \frac{\frac{\partial }{\partial \theta }f(x;\theta )}{f(x;\theta )}f(x;\theta )\mathrm{d}x=\frac{\partial }{\partial \theta }\int f(x;\theta )\mathrm{d}x=\frac{\partial }{\partial \theta }1=0.$$

Thus, the Fisher information can be written as

$$I(\theta )=\mathbb{E}\left[{\left(\frac{\partial }{\partial \theta }\log f(X;\theta )\right)}^2\right]$$

Further, for a well-specified model under similar regularity conditions, we can show that

$$I(\theta )=-\mathbb{E}\left[\frac{{\partial }^2}{\partial {\theta }^2}\log f(X;\theta )\right],$$

because

$$\begin{array}{rl}\frac{{\partial }^2}{\partial {\theta }^2}\log f(X;\theta )& =\frac{\frac{{\partial }^2}{\partial {\theta }^2}f(X;\theta )}{f(X;\theta )}-{\left(\frac{\frac{\partial }{\partial \theta }f(X;\theta )}{f(X;\theta )}\right)}^2\\ & =\frac{\frac{{\partial }^2}{\partial {\theta }^2}f(X;\theta )}{f(X;\theta )}-{\left(\frac{\partial }{\partial \theta }\log f(X;\theta )\right)}^2,\end{array}$$

and the expectation of the first term is zero.

Fisher Information Matrix

The Fisher information matrix is the Covariance matrix of the score function:

$$I(\theta )=\mathbb{E}\left[s(\theta )s(\theta {)}^T\right]-\mathbb{E}[s(\theta )]\mathbb{E}[s(\theta ){]}^T,$$

where $s(\theta )$ is the Score Function.

Information Curvature

The Fisher information encodes information each random variable carries about the parameter. Specifically, under well-specification, $-I(\theta )$ is the expected curvature of the log-likelihood function at $\theta$.

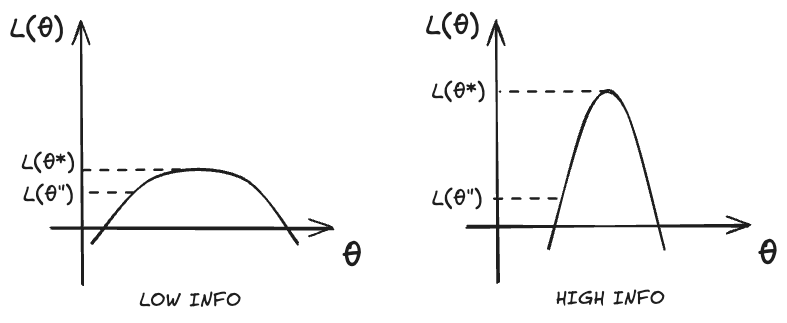
When the Fisher information is small, we have a flat log-likelihood curve, making it harder for the stochastic estimator to find the maximum likelihood estimate; when the Fisher information is large, we have a steep log-likelihood curve, making it easier for the stochastic estimator to find the maximum likelihood estimate.